スポンサードリンク
2024年 芝浦工業大学(2月2日) 数学 4.
- まろりん
- 2024年2月4日
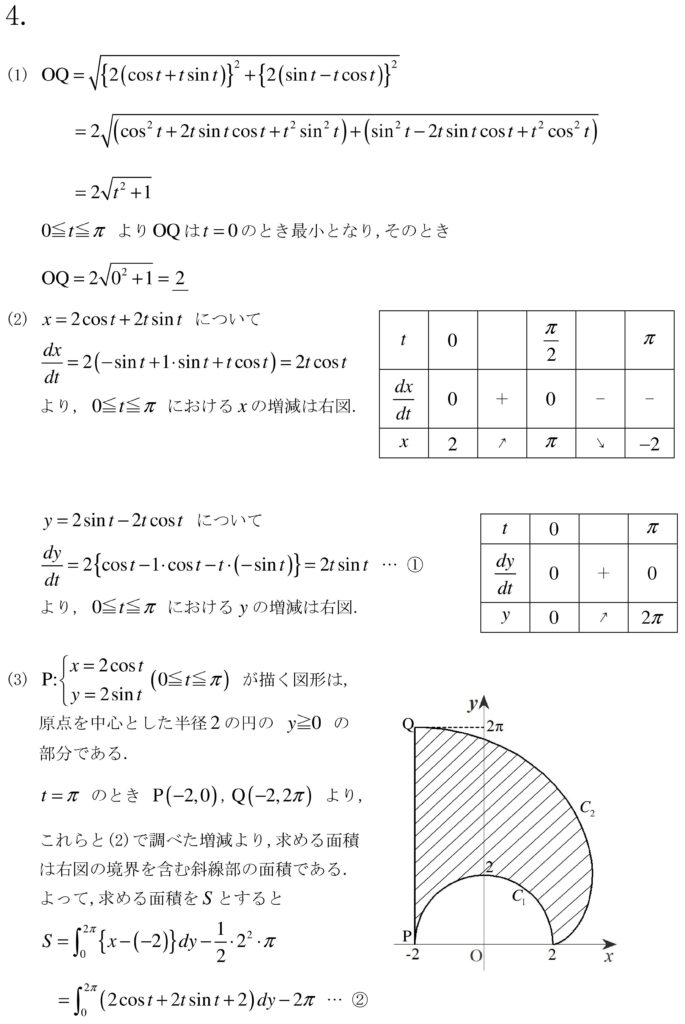

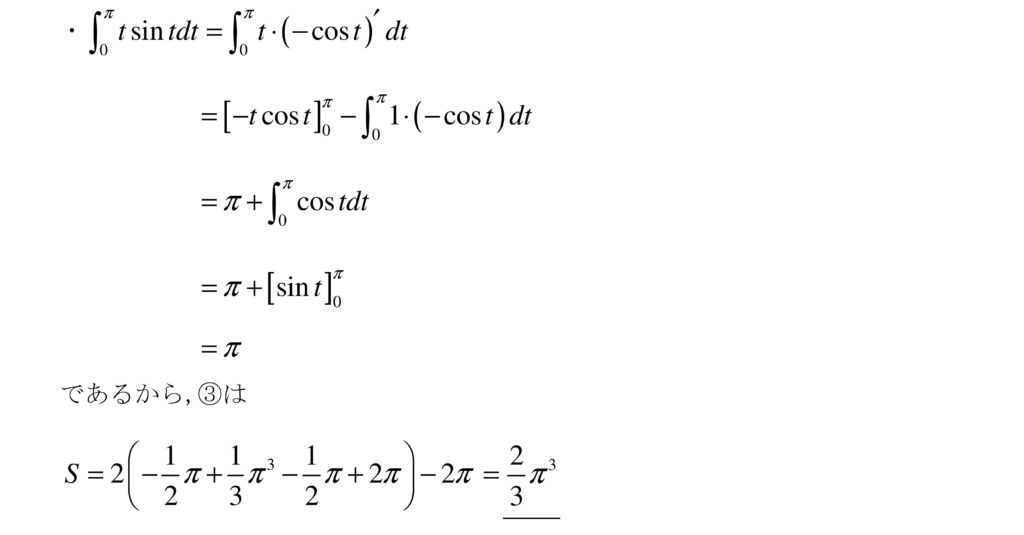
(2)までは丁寧に計算して落とさないようにしたい。
(3)はdxで積分すると2<xの部分の引くところが面倒そうなので,dyで積分する方でやって、それでも面倒かな、とも思ったが、部分積分の結果同じ積分や、0になる式が出てきて意外と計算は難しくなかった。
※(3)を2025.01.30に修正しました。
※(3)を2025.12.02に再度修正しました。
スポンサードリンク


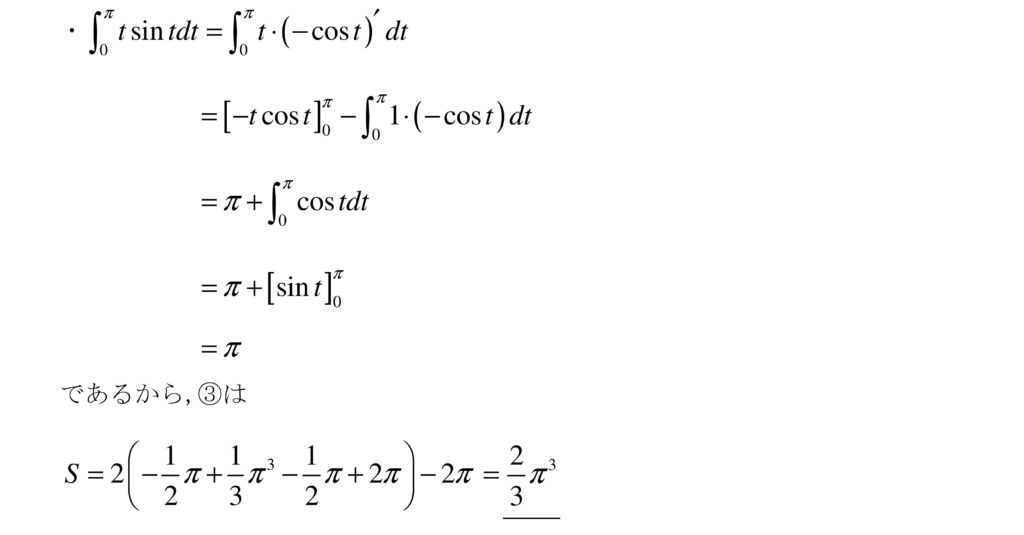
(2)までは丁寧に計算して落とさないようにしたい。
(3)はdxで積分すると2<xの部分の引くところが面倒そうなので,dyで積分する方でやって、それでも面倒かな、とも思ったが、部分積分の結果同じ積分や、0になる式が出てきて意外と計算は難しくなかった。
※(3)を2025.01.30に修正しました。
※(3)を2025.12.02に再度修正しました。
フマキラー2024年4月22日 11:21 /
受験生です。いつも使わせていただいてます。 質問なのですが、(3)の極方程式の面積の公式で、tは偏角じゃないのに使っていいんですか? r=f(θ)のθはtanθ=y/xを満たしてないと極方程式にならないと思ったのですが...